مشتق / مشتق توابع نمائی
در این مبحث, مسایلی را مورد بحث قرار میدهیم که جواب آنها اکسترمم مطلق یک تابع روی یک بازه بسته است.
در این مسایل از قضیه اکسترمم استفاده می شود که وجود یک مقدار ماکسیمم مطلق و یک مقدار مینیمم مطلق را برای تابعی روی یک بازه بسته تضمین میکند، به شرطی که تابع روی آن بازه بسته پیوسته باشد. این روش را با چند مثال نمایش میدهیم.
مثال 1: یک سازنده جعبه، می خواهد از تکه مقواهایی که باید بریده شوند برابر12 اینچ مربع با بریدن چهار مربع متساوی از چهار گوشه هریک، و بالازدن جوانب آن , جعبه سرباز بسازد. طول ضلع مربع هایی که باید بریده شوند چقدر باشد تا حجم جعبه به حداکثر ممکن برسد؟
حل: فرض کنید طول ضلع هریک از مربع هایی که باید بریده شوند چقدر باشد تا حجم جعبه اینج مکعب باشد. طول ابعاد جعبه, برحسب اینج برابر است با
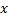 ،
،
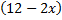 ,
,
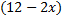 . شکل زیر یک تکه مقوای داده شده را نشان می دهد
. شکل زیر یک تکه مقوای داده شده را نشان می دهد

و شکل زیر جعبه مطلوب را.
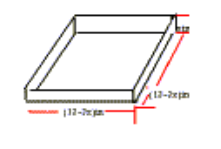
حجم جعبه برابر حاصلضرب سه بعد آن است لذا
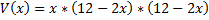
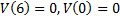
مقدار
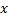 مورد نظر در بازه بسته
مورد نظر در بازه بسته
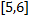 قرار دارد. چون
قرار دارد. چون
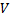 روی بازه بسته
روی بازه بسته
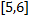 پیوسته است, از قضیه اکسترمم نتیجه می شود که روی این بازه
پیوسته است, از قضیه اکسترمم نتیجه می شود که روی این بازه
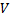 دارای یک مقدار ماکسیمم مطلق است. همچنین میدانیم که این مقدار ماکسیمم مطلق یا به ازای یک عدد بحرانی به دست می آید و یا به ازای یکی از نقاط انتهایی. برای محاسبه اعداد بحرانی
دارای یک مقدار ماکسیمم مطلق است. همچنین میدانیم که این مقدار ماکسیمم مطلق یا به ازای یک عدد بحرانی به دست می آید و یا به ازای یکی از نقاط انتهایی. برای محاسبه اعداد بحرانی
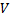 ابتدا
ابتدا
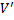 را محاسبه مکنیم و حالاتی که
را محاسبه مکنیم و حالاتی که
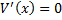 یا
یا
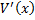 وجود ندارد را به دست میآوریم . از معادله قبل داریم:
وجود ندارد را به دست میآوریم . از معادله قبل داریم:
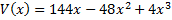
بنابراین
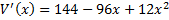
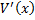 به ازای تمام مقادیر
به ازای تمام مقادیر
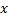 وجود دارد. اگر
وجود دارد. اگر
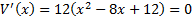 و از آن نتیجه می شود. که
و از آن نتیجه می شود. که
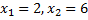 . اعداد بحرانی
. اعداد بحرانی
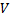 عبارتند از 2 و 6 و هر دو در بازه بسته
عبارتند از 2 و 6 و هر دو در بازه بسته
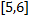 هستند. مقدار ماکسیمم مطلق
هستند. مقدار ماکسیمم مطلق
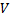 یا به ازای یک عدد بحرانی به دست می آید و یا به ازای یکی از نقاط انتهایی چون
یا به ازای یک عدد بحرانی به دست می آید و یا به ازای یکی از نقاط انتهایی چون
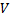 و مقدار ماکسیمم مطلق
و مقدار ماکسیمم مطلق
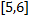 روی
روی
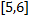 عدد 128 است که در 2 به دست می آید. پس بیشترین حجم ممکن 128 اینچ مکعب است و این مقدار وقتی به دست می اید که طول ضلع مربع هایی که باید بریده شوند برابر با 2 اینج باشد.
عدد 128 است که در 2 به دست می آید. پس بیشترین حجم ممکن 128 اینچ مکعب است و این مقدار وقتی به دست می اید که طول ضلع مربع هایی که باید بریده شوند برابر با 2 اینج باشد.
مثال 2: دو نقطه
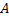 و
و
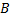 در دو طرف یک رودخانه مستقیم به عرض 3 کیلومتر مقابل هم قرار دارند. نقطه
در دو طرف یک رودخانه مستقیم به عرض 3 کیلومتر مقابل هم قرار دارند. نقطه
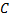 که 2 کیلومتر از نقطه
که 2 کیلومتر از نقطه
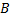 فاصله دارد, در همان طرف از رودخانه واقع است که نقطه
فاصله دارد, در همان طرف از رودخانه واقع است که نقطه
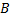 . یک شرکت تلفن میخواهد از
. یک شرکت تلفن میخواهد از
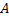 به
به
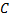 کابل بکشد. اگر هزینه هرکیلومتر کابل در زیر آب 25 درصد بیش از هزینه کابل روی زمین باشد. کدام خط کابل برای شرکت مقرون به صرفه تر است.
کابل بکشد. اگر هزینه هرکیلومتر کابل در زیر آب 25 درصد بیش از هزینه کابل روی زمین باشد. کدام خط کابل برای شرکت مقرون به صرفه تر است.
حل: به شکل زیر رجوع کنید.
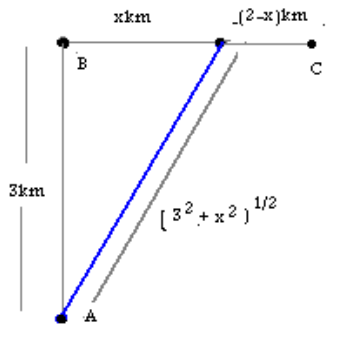
فرض کنید نقطه ای چون
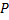 واقع در ساحل مشترک
واقع در ساحل مشترک
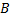 و
و
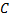 بین
بین
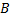 و
و
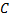 در جایی است که کابل از
در جایی است که کابل از
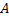 به
به
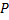 و از آنجا به
و از آنجا به
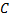 میرود . و فرض کنید فاصله بین
میرود . و فرض کنید فاصله بین
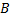 تا
تا
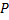 ,
,
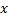 کیلومتر باشد. پس فاصله بین
کیلومتر باشد. پس فاصله بین
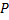 تا
تا
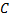 ,
,
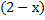 کیلومتر است و
کیلومتر است و
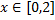 . فرض کنید هزینه هر کیلومتر کابل روی زمین
. فرض کنید هزینه هر کیلومتر کابل روی زمین
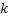 تومان و هزینه هرکیلومتر کابل زیر اب
تومان و هزینه هرکیلومتر کابل زیر اب
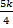 تومان باشد (
تومان باشد (
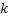 مقداری ثابت). اگر
مقداری ثابت). اگر
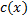 تومان کل هزینه کابل از
تومان کل هزینه کابل از
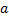 تا
تا
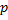 و از
و از
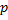 تا
تا
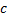 باشد. داریم.
باشد. داریم.
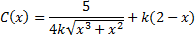 چون
چون
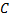 بر
بر
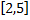 پیوسته است، می توانیم از قضیه اکسترمم استفاده کنیم، لذا روی
پیوسته است، می توانیم از قضیه اکسترمم استفاده کنیم، لذا روی
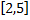 هم مقدار ماکسیمم مطلق دارد و هم مقدار مینیمم مطلق. در اینجا منظور ما یافتن مقدار مینیمم مطلق است.
هم مقدار ماکسیمم مطلق دارد و هم مقدار مینیمم مطلق. در اینجا منظور ما یافتن مقدار مینیمم مطلق است.
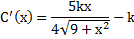
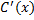
به ازای همه مقادیر
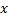 وجود دارد. اگر بنویسیم
وجود دارد. اگر بنویسیم
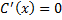 و معادله را نسبت به
و معادله را نسبت به
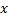 حل کنیم داریم
حل کنیم داریم
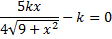
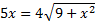
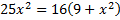
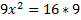
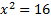
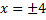
عدد 4- یک ریشه اضافی معادله بالا است و 4- هم در بازه
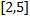 قرار ندارد. بنابراین عدد c در
قرار ندارد. بنابراین عدد c در
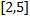 نیست. لذا مقدار مینیمم مطلق c بر
نیست. لذا مقدار مینیمم مطلق c بر
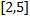 باید به ازای یکی از نقاط انتهایی بازه به دست آید.
حال
باید به ازای یکی از نقاط انتهایی بازه به دست آید.
حال
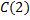 و
و
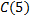 را محاسبه می کنیم
را محاسبه می کنیم
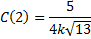
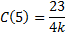
چون مقدار
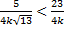 مقدار مینیمم مطلق
C
روی
مقدار مینیمم مطلق
C
روی
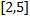 عدد
عدد
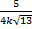 است که به ازای
است که به ازای
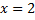 به دست میآید. پس، برای صرف کمترین هزینه باید کابل در زیر آب و به طور مستقیم از
A
تا
C
کشیده شود
به دست میآید. پس، برای صرف کمترین هزینه باید کابل در زیر آب و به طور مستقیم از
A
تا
C
کشیده شود
1. مطلوب است محاسبه مساحت بزرگترین مستطیلی که محیط آن 255 سانتیمتر است.
2. مطلوب است محاسبه مساحت بزرگترین مثلث متساوی الساقین که محیط آن 18 سانتی متر است.
3. مطلوب است عددی از بازه [1,5] که تفاضل بین آن عدد و مربعش ماکسیمم باشد.
4. مطلوب است عددی از بازه [1/3,2] که مجموع ان عدد و عکسش ماکسیمم باشد.
5. مطلوب است مساحت بزرگترین مستطیلی که دو راس آن محور x ها باشد، دو راس دیگرهم روی یا بالای محور x ها باشد و هم روی سهمی
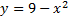
6. مطلوب است مساحت بزرگترین مستطیل قابل محاط در یک دایره به شعاع r .
7. یک سازنده قوطی حلبی، با بریدن مربع های متساوی از چهار گوشه ورق های حلبی به ابعاد 8 اینچ و 15 اینچ و بریدن چهار طرف آن قوطی های سرباز می سازد. مطلوب است طول ضلع مربع هایی که باید بریده شود، تا حجم قوطی ساخته شده بیشترین مقدار ممکن باشد
8. میخواهیم اطراف قطعه زمین مستطیل شکلی را نرده بکشیم و سپس با نرده دیگری ان را از وسط نصف کنیم. اگر بهای هر فوت نرده وسطی دو دلار و بهای هر فوت نرده دیگر پنج دلار باشد، مطلوب است ابعاد قطعه زمینی با بیشترین مساحت ممکن که بتوان آن را با 965 دلار نرده کشی کرد.
9. می خواهیم سه طرف قطعه زمین مستطیل شکلی را که یک طرف آن رودخانه است و به عنوان حصار طبیعی محسوب می شود، نرده بکشیم. با این شرایط ابعاد بزرگترین قطعه زمین را بیابید که بتوان با 25 متر نرده محصور شود.
10. برای اینکه بسته ای با پست فرستاده شود، مجموع طول کمر ( محیط یک مقطع عرضی) آن نباید از 100 اینچ تجاوز کند میخواهیم بسته ای به شکل مکعب مستطیل را که مقطع عرضی آن مربع است با پست بفرستیم. با این شرایط، ابعاد بسته ای را که دارای بزرگترین حجم ممکن است بیابید.
11. جزیره ای در نقطه ای چون A واقع است که 6 کیلومتر از B ، نزدیکترین نقطه یک ساحل مستقیم به A ، فاصله دارد. شخصی که ساکن جزیره است میخواهد به نقطه ای چون C برود که در ساحل قرار دارد و در امتداد ساحل فاصله آن تا B ، 9 کیلومتر است. این شخص می تواند قایقی با ترخ هر کیلومتر 25 دلار کرایه کند و با آن تا نقطه ای چون P واقع بین B و C برود. از انجا، از طریق یک جاده مستقیم، با یک تاکسی با نرخ هر کیلومتر 2 دلار خود را به C برساند. از A به C ارزانترین راه کدام است.
12. تمرین 11 را در حالتی که فاصله CB و در امتداد ساحل تنها 7 کیلومتر باشد، حل کنید.
13. مثال 2 ی این بخش را درصورتی که فاصله نقطه C تا B در امتداد رودخانه 6 کیلومتر باشد، حل کنید.
14. مثال 2 و تمرین های 11، 12، و 13 حالت های خاصی از مساله کلیر تر زیرند:
فرض کنید
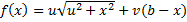 که در آن
x در
که در آن
x در
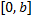 است و
است و
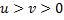 . نشان دهید برای اینکه مقدار مینیمم مطلق
. نشان دهید برای اینکه مقدار مینیمم مطلق
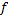 به ازای عددی از بازه باز
به ازای عددی از بازه باز
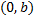 به دست می آید، نامساوی
به دست می آید، نامساوی
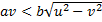 باید برقرار باشد.
باید برقرار باشد.
15. اگر برد گلوله ای
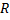 فوت باشد، انگاه
فوت باشد، انگاه
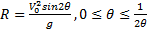 که در آن
که در آن
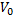 سرعت اولیه بر حسب فوت بر ثانیه،
سرعت اولیه بر حسب فوت بر ثانیه،
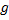 شتاب ثقل بر حسب فوت بر مربع ثانیه، و
θ اندازه زاویه بین لوله تفنگ و افق بر حسب رادیان است. مقدار θ چقدر باشد تا برد ماکسیمم باشد.
شتاب ثقل بر حسب فوت بر مربع ثانیه، و
θ اندازه زاویه بین لوله تفنگ و افق بر حسب رادیان است. مقدار θ چقدر باشد تا برد ماکسیمم باشد.

