مشتق / مشتق مراتب بالا
اگر
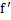 مشتق تابع
مشتق تابع
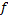 باشد, انگاه
باشد, انگاه
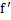 نیز خود یک تابع است و مشتق اول نامیده می شود. اگر مشتق وجود داشته باشد, آن را مشتق دوم می نامیم و با علامت
نیز خود یک تابع است و مشتق اول نامیده می شود. اگر مشتق وجود داشته باشد, آن را مشتق دوم می نامیم و با علامت
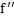 نمایش میدهیم.
( که خوانده می شود اف زگوند ) به طور مشابه مشتق سوم
نمایش میدهیم.
( که خوانده می شود اف زگوند ) به طور مشابه مشتق سوم
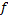 را به عنوان مشتق اول
را به عنوان مشتق اول
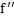 در صورت وجود تعریف کرده و با علامت
در صورت وجود تعریف کرده و با علامت
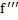 نشان میدهیم ( و می خوانیم اف تیرس ).
نشان میدهیم ( و می خوانیم اف تیرس ).
اگر
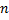 یک عدد صحیح مثبت بزرگتر از 1 باشد , مشتق
یک عدد صحیح مثبت بزرگتر از 1 باشد , مشتق
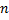 م تابع
م تابع
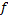 رابه عنوان مشتق اول
رابه عنوان مشتق اول
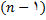 م تابع تعریف میکنیم و آن را با علامت
م تابع تعریف میکنیم و آن را با علامت
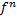 نشان میدهیم.
پس میتوانیم خود تابع
نشان میدهیم.
پس میتوانیم خود تابع
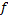 را با
را با
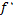 نیز نمایش دهیم. علامت دیگری برای مشتق
نیز نمایش دهیم. علامت دیگری برای مشتق
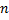 ام به صورت
ام به صورت
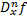 به وسیله
به وسیله
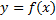 تعریف شده باشد مشتق
تعریف شده باشد مشتق
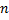 ام
را با علامت
ام
را با علامت
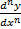 نیز میتوان نشان داد.
نیز میتوان نشان داد.
مثال 1: اگر تابع به صورت
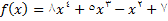 تعریف شده باشد تمام مشتق های
تعریف شده باشد تمام مشتق های
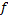 را پیدا کنید.
را پیدا کنید.
حل:
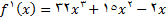
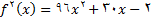
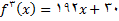
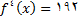
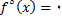
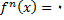
چون
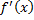 آهنگ تغیر
آهنگ تغیر
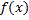 در یک واحد از تغییر
در یک واحد از تغییر
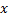 را به دست میدهد,
را به دست میدهد,
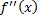 , که مشتق
, که مشتق
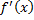 است, آهنگ تغیر
است, آهنگ تغیر
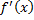 در یک واحد از تغییر
در یک واحد از تغییر
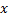 را به دست میدهد.
اگر
را به دست میدهد.
اگر
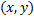 نقطه ای روی نمودار
نقطه ای روی نمودار
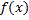 باشد, آنگاه
باشد, آنگاه
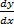 ضریب زاویه خط مماس بر نمودار در نقطه
ضریب زاویه خط مماس بر نمودار در نقطه
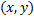 می باشد. بنابراین
می باشد. بنابراین
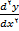 آهنگ تغییر ضریب زاویه خط مماس نسبت
به x در نقطه
آهنگ تغییر ضریب زاویه خط مماس نسبت
به x در نقطه
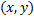 است.
است.
مثال 2: فرض کنید
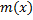 ضریب زاویه خط مماس بر منحنی
ضریب زاویه خط مماس بر منحنی
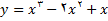 در نقطه
در نقطه
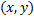 باشد. آهنگ لحظه ای تغییر
باشد. آهنگ لحظه ای تغییر
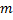 در یک واحد از تغییر
در یک واحد از تغییر
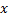 در نقطه
در نقطه
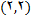 را پیداکنید.
را پیداکنید.
حل:
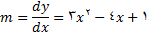
اهنگ لحظه ای تغییر
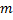 در یک واحد از تغیر
در یک واحد از تغیر
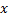 برابر با
برابر با
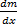 یا به عبارت دیگر
یا به عبارت دیگر
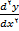 است.
است.
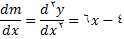
در نقطه
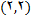 , داریم
, داریم
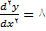 . بنابراین , در نقطه
. بنابراین , در نقطه
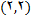 تغییر
تغییر
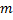 8 برابر تغییر
8 برابر تغییر
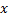 است.
است.
مشتق دوم یعنی
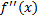 بر حسب واحد
بر حسب واحد
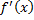 در واحد
در واحد
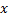 بیان میشود, که عبارت است از واحد
بیان میشود, که عبارت است از واحد
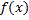 در واحد
در واحد
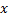 در واحد
در واحد
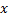 ( مربع واحد ) . مثلا در حرکت مستقیم الخط, اگر در لحظه
( مربع واحد ) . مثلا در حرکت مستقیم الخط, اگر در لحظه
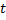 ( ثانیه ) فاصله از مبدا
( ثانیه ) فاصله از مبدا
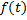 سانتیمتر باشد, سرعت ذره در لحظه
سانتیمتر باشد, سرعت ذره در لحظه
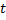 ,
,
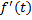 سانتیمتر در ثانیه و آهنگ لحظه ای تغییر سرعت در
سانتیمتر در ثانیه و آهنگ لحظه ای تغییر سرعت در
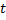 ( ثانیه ),
( ثانیه ),
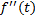 سانتیمتر بر مربع ثانیه می باشد. در فیزیک آهنگ لحظه ای تغییر سرعت را شتاب لحظه ای می نامند بنابراین اگر ذره ای در امتداد یک خط مستقیم طبق معادله
سانتیمتر بر مربع ثانیه می باشد. در فیزیک آهنگ لحظه ای تغییر سرعت را شتاب لحظه ای می نامند بنابراین اگر ذره ای در امتداد یک خط مستقیم طبق معادله
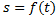 در حال حرکت باشد و در لحظه
در حال حرکت باشد و در لحظه
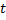 (ثانیه ) سرعت لحظه ای
(ثانیه ) سرعت لحظه ای
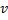 سانتیمتر در ثانیه و شتاب
سانتیمتر در ثانیه و شتاب
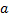 سانتیمتر بر مربع ثانیه باشد, آنگاه
سانتیمتر بر مربع ثانیه باشد, آنگاه
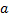 برابر با مشتق
برابر با مشتق
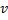 نسبت به
نسبت به
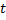 و یا مشتق دوم
و یا مشتق دوم
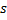 نسبت به
نسبت به
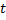 خواهد بود. یعنی
خواهد بود. یعنی
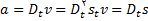
وقتی که
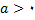 افزایش می یابد و وقتی که
افزایش می یابد و وقتی که
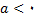 کاهش می یابد وقتی که
کاهش می یابد وقتی که
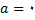 تغییر نمیکند. چون مقدار سرعت یک ذره در لحظه
تغییر نمیکند. چون مقدار سرعت یک ذره در لحظه
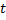 (ثانیه) برابر
(ثانیه) برابر
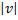 سانتیمتر بر ثانیه است , نتایج زیر را داریم.
سانتیمتر بر ثانیه است , نتایج زیر را داریم.
1. اگر
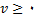 و
و
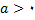 ,مقدار سرعت در حال افزایش است
,مقدار سرعت در حال افزایش است
2. اگر
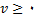 و
و
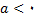 ,مقدار سرعت در حال کاهش است
,مقدار سرعت در حال کاهش است
3. اگر
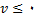 و
و
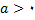 ,مقدار سرعت در حال کاهش است
,مقدار سرعت در حال کاهش است
4. اگر
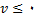 و
و
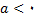 ,مقدار سرعت در حال افزایش است
,مقدار سرعت در حال افزایش است
مثال3: ذره ای در امتداد یک خط مستقیم طبق معادله حرکت زیر حرکت میکند.
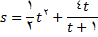
که در آن
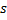 سانتیمتر, فاصله جهت دار ذره از مبدا در لحظه
سانتیمتر, فاصله جهت دار ذره از مبدا در لحظه
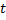 ( ثانیه ) می باشد.
اگر
( ثانیه ) می باشد.
اگر
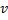 سانتیمتر در ثانیه, سرعت لحظه ای و
سانتیمتر در ثانیه, سرعت لحظه ای و
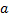 سانتیمتر بر مربع ثانیه شتاب لحظه ای در لحظه
سانتیمتر بر مربع ثانیه شتاب لحظه ای در لحظه
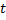 ( ثانیه ) باشد. مقادیر
( ثانیه ) باشد. مقادیر
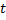 و
و
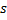 و
و
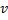 را وقتی
را وقتی
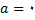 به دست آورید.
به دست آورید.
حل:
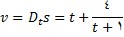
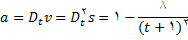
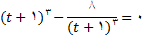
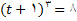
چون تنها مقدار حقیقی
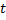 از ریشه سوم 8 به دست می آید, بنابراین
از ریشه سوم 8 به دست می آید, بنابراین
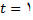 یا
یا
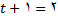
وقتی که
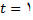
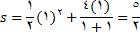
و
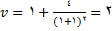
بنابراین, در ثانیه 1 شتاب صفر و این موقعی است که ذره از مبدا 2.5 سانتیمتر فاصله دارد و با سرعت 2 سانتیمتر در ثانیه به طرف راست درحرکت است.
کاربردهای دیگر مشتق دوم, موارد استفاده آن در پیدا کردن اکسترمم ( مینیمم یا ماکسیمم) نسبی توابع در رسم نمودار تابع است.
کاربرد مهمی از مشتقهای مراتب بالاتر, استفاده از انها در بسط توابع به صورت سری نامتناهی است که در بخشهای بعدی خواهیم دید.
مثال 4: ثابت کنید
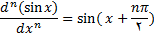
حل: برای اثبات رابطه فوق از استقرا ریاضی و فرمولهای زیر استفاده میکنیم
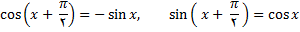
ابتدا نشان میدهیم که معادله فوق برای
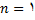 درست است.
درست است.
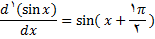
بنابراین به ازای
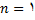 برقرار است. حال فرض میکنیم که معادله فوق به ازای
برقرار است. حال فرض میکنیم که معادله فوق به ازای
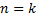 درست باشد. ثابت می کنیم که به ازای
درست باشد. ثابت می کنیم که به ازای
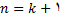 نیز درست است.
بنابراین فرض میکنیم که
نیز درست است.
بنابراین فرض میکنیم که
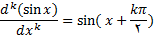
باید ثابت کنیم
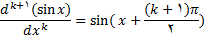
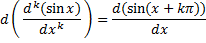
میتوان نوشت.
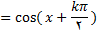
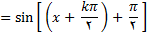
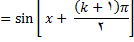
در هر یکی ازتمرین های زیر, مشتق اول و دوم تابع تعریف شده با معادله مفروض را به دست اورید.
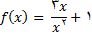
2.
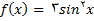
3.
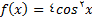
4.
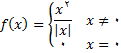
مقدار
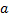 و
و
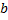 و
و
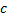 را طوری بیابید که
را طوری بیابید که
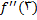 موجود باشد.
موجود باشد.


