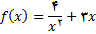مشتق / مشتق تابع اف
مشتق تابع
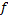 تابعی است که با علامت
تابعی است که با علامت
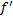 نشان داده می شود و مقدار آن در هر عدد واقع در قلمرو
نشان داده می شود و مقدار آن در هر عدد واقع در قلمرو
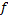 به صورت زیر نشان داده می شود.
به صورت زیر نشان داده می شود.
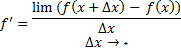 (1)
(1)
به شرطی که حد فوق وجود داشته باشد. علامت دیگری که به جای
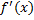 به کار برده می شود,
به کار برده می شود,
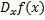 است که خوانده می شود مشتق اف اکس نسبت به اکس. اگر
است که خوانده می شود مشتق اف اکس نسبت به اکس. اگر
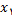 عدد خاصی از قلمرو
عدد خاصی از قلمرو
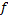 باشد, آنگاه داریم
باشد, آنگاه داریم
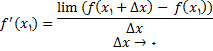 (2)
(2)
به شرطی که حد فوق وجود داشته باشد. اگر فرمولهای (1) و (2) را با هم مقایسه کنیم, متوجه می شویم که ضریب زاویه خط مماس بر نمودار
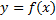 در نقطه
در نقطه
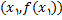 دقیقا برابر با مشتق
تابع
دقیقا برابر با مشتق
تابع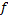 در
در 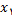 است.
است.
مثال 1 : تابع
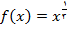 مفروض است
مفروض است
(الف) 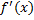 را به دست اورید
را به دست اورید
(ب) نشان دهید
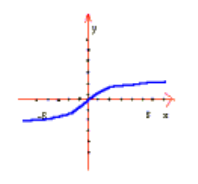
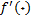 وجود ندارد حتی اگر در 0 پیوسته است. نمودار تابع
وجود ندارد حتی اگر در 0 پیوسته است. نمودار تابع
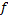 را رسم کنید.
را رسم کنید.
حل:
(الف)
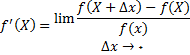
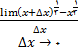 =
=
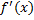
صورت کسر فوق را برای به دست اوردن عامل مشترک
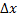 در صورت و مخرج گویا می کنیم و خواهیم داشت.
در صورت و مخرج گویا می کنیم و خواهیم داشت.
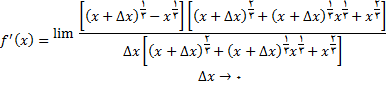
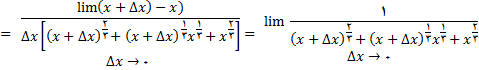
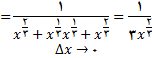
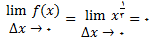
1. تمرین
در تمرین های زیر, با استفاده از فرمول (1) ی این بخش,
تمرین
در تمرین های زیر, با استفاده از فرمول (1) ی این بخش, 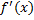 را برای تابع داده شده محاسبه کنید
را برای تابع داده شده محاسبه کنید
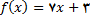
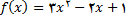
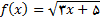
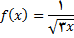
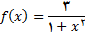
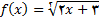
2.در تمرین های زیر, با استفاده از فرمول (2) ی این بخش, 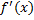 را برای
را برای
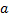 داده شده محاسبه کنید
داده شده محاسبه کنید
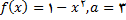
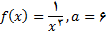
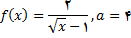
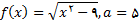
3.در تمرین های زیر
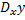 را به دست آورید.
را به دست آورید.