ریاضی عمومی / پیوستگی روی یک بازه
در بخش قبل نشان دادیم که تابع
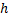 با ضابطه
با ضابطه
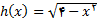 به ازای هر عدد واقع در بازه باز
به ازای هر عدد واقع در بازه باز
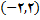 پیوسته است. به دلیل این واقعیت گوییم که تابع
پیوسته است. به دلیل این واقعیت گوییم که تابع
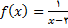 روی بازه باز
روی بازه باز
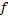 پیوسته است. تعریف کلی پیوستگی روی یک بازه به صورت زیر است
پیوسته است. تعریف کلی پیوستگی روی یک بازه به صورت زیر است
تعریف1 : گفته میشود که تابعی روی یک بازه باز پیوسته است اگر و تنها اگر آن تابع به ازای هرعدد واقع در آن بازه باز پیوسته باشد.
مثال1 : تابع
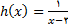 روی کدام بازه باز پیوسته است؟
روی کدام بازه باز پیوسته است؟
حل: تابع
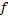 به ازای هر عدد بجز 3 پیوسته است. پس بنا به تعریف
به ازای هر عدد بجز 3 پیوسته است. پس بنا به تعریف
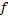 روی هر بازه بازی که شامل عدد 3 نباشد پیوسته است. دوباره به تابع
روی هر بازه بازی که شامل عدد 3 نباشد پیوسته است. دوباره به تابع
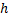 با ضابطه
با ضابطه
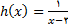 مراجعه میکنیم می دانیم که
مراجعه میکنیم می دانیم که
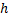 روی بازه باز
روی بازه باز
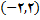 پیوسته است . ولی چون
پیوسته است . ولی چون
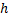 روی هیچ بازه بازی که شامل
روی هیچ بازه بازی که شامل
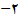 یا 4 باشد تعریف نشده است در مورد
یا 4 باشد تعریف نشده است در مورد
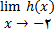 یا
یا
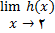 نمی توان چیزی گفت از اینرو برای بحث در مساله پیوستگی
نمی توان چیزی گفت از اینرو برای بحث در مساله پیوستگی
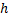 روی بازه بسته
روی بازه بسته
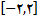 باید مفهوم پیوستگی را گسترش دهیم تا پیوستگی در انتهای یک بازه بسته را در بر گیرد. برای این کار ابتدا پیوستگی از طرفین را تعریف می کنیم.
باید مفهوم پیوستگی را گسترش دهیم تا پیوستگی در انتهای یک بازه بسته را در بر گیرد. برای این کار ابتدا پیوستگی از طرفین را تعریف می کنیم.
تعریف2 : گفته میشود که تابع
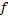 از طرف راست در عدد
از طرف راست در عدد
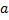 پیوسته است اگر و تنها اگر سه شرط زیر برقرار باشد.
پیوسته است اگر و تنها اگر سه شرط زیر برقرار باشد.
1 - مقدار 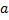 وجود داشته باشد.
وجود داشته باشد.
2 – حد 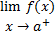 جود داشته باشد.
جود داشته باشد.
3 – 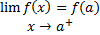
تعریف3 : گفته می شود که تابع
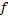 از طرف چپ در
از طرف چپ در
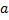 عدد پیوسته است اگر و تنها اگر سه شرط زیر برقرار باشد.
عدد پیوسته است اگر و تنها اگر سه شرط زیر برقرار باشد.
1 - مقدار 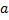 وجود داشته باشد.
وجود داشته باشد.
2 – حد 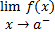 وجود داشته باشد.
وجود داشته باشد.
3 – 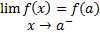
تعریف 4 : چنانچه قلمرو تابعی شامل بازه بسته
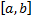 باشد. که آن تابع روی
باشد. که آن تابع روی
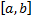 پیوسته است, اگر و تنها اگر روی بازه باز
پیوسته است, اگر و تنها اگر روی بازه باز
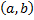 پیوسته باشد و همچنین از طرف راست در
پیوسته باشد و همچنین از طرف راست در
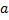 و از طرف چپ در
و از طرف چپ در
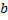 پیوسته باشد.
پیوسته باشد.
مثال 2 : اگر داشته باشیم
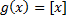 در مورد پیوستگی تابع
در مورد پیوستگی تابع
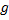 بحث کنید.
بحث کنید.
حل: شکل زیر نمودار را نشان میدهد.
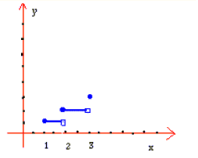
فرض کنید عددی در بازه
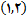 باشد. در اینصورت
باشد. در اینصورت
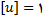 , و در نتیجه
, و در نتیجه
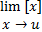 . از اینرو اگر
. از اینرو اگر
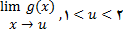 بنابراین
بنابراین
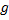 روی بازه
(1,2]
پیوسته است.
روی بازه
(1,2]
پیوسته است.
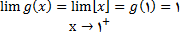
بنابراین
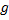 از طرف راست در 1 پیوسته است اما داریم
از طرف راست در 1 پیوسته است اما داریم
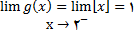
و چون
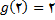 , پس از طرف چپ در 2 پیوسته نیست. بنابراین , تابع
, پس از طرف چپ در 2 پیوسته نیست. بنابراین , تابع
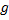 روزی بازه نیمه باز
روزی بازه نیمه باز
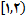 از طرف راست پیوسته است.
به طور مشابه دیده میشود که
از طرف راست پیوسته است.
به طور مشابه دیده میشود که
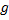 در هر عدد
در هر عدد 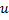 که
که
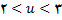 پیوسته است . در 2 ,
پیوسته است . در 2 ,
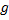 از طرف راست پیوسته است زیرا
از طرف راست پیوسته است زیرا
 , ولی از طرف چپ در 3 پیوسته نیست زیرا
, ولی از طرف چپ در 3 پیوسته نیست زیرا
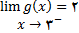 و
و
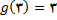 . از اینرو
. از اینرو
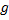 روی بازه
روی بازه
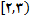 نیز پیوسته است.
اکنون قضیه مهمی را در بازه تابعی که روی یک بازه بسته پیوسته است , مورد بحث قرار میدهیم. این قضیه مقدار میانی نامیده می شود و در بخشهای بعدی مورد نیاز است.
نیز پیوسته است.
اکنون قضیه مهمی را در بازه تابعی که روی یک بازه بسته پیوسته است , مورد بحث قرار میدهیم. این قضیه مقدار میانی نامیده می شود و در بخشهای بعدی مورد نیاز است.
قضیه مقدار میانی: اگر تابع
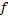 روی بازه بسته
روی بازه بسته
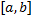 پیوسته باشد و اگر
پیوسته باشد و اگر
 , آنگاه به ازای هر عدد بین
, آنگاه به ازای هر عدد بین
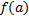 و
و
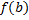 , عددی مانند
, عددی مانند
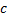 بین
بین
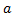 و
و
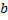 وجود دارد به طوری که
وجود دارد به طوری که
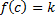 .
.
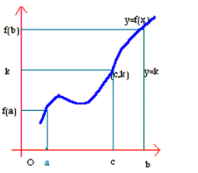
در شکل زیر
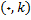 نقطه ای دلخواه روی محور
نقطه ای دلخواه روی محور
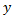 ها بین نقاط
ها بین نقاط
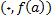 و
و
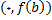 است. قضیه میگوید که خط
است. قضیه میگوید که خط
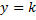 باید منحنی به معادله
باید منحنی به معادله
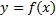 را در نقطه
را در نقطه
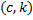 قطع کند, که بین
قطع کند, که بین
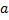 و
و
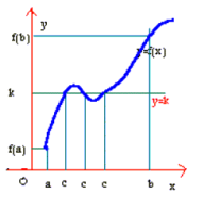
 واقع است. شکل زیر این تقاطع را نشان میدهد.
واقع است. شکل زیر این تقاطع را نشان میدهد.
دقت کنید که ممکن است به ازای بعضی از مقادیر
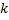 بیش از یک مقدار
بیش از یک مقدار
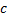 وجود داشته باشد. قضیه میگوید که همیشه, حداقل یک مقدار برای
وجود داشته باشد. قضیه میگوید که همیشه, حداقل یک مقدار برای
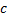 وجود دارد ولی این مقدار, لزوما یکتا نیست. شکل زیر, سه مقدار ممکن
وجود دارد ولی این مقدار, لزوما یکتا نیست. شکل زیر, سه مقدار ممکن
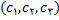 به ازای یک مقدار خاص
به ازای یک مقدار خاص
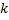 را نشان می دهد.
را نشان می دهد.
قضیه میگوید که اگر تابع
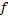 روی یک بازه بسته
روی یک بازه بسته
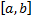 پیوسته باشد, آنگاه وقتی
پیوسته باشد, آنگاه وقتی
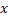 همه مقادیر بین
همه مقادیر بین
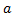 و
و
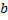 را اختیار میکند, هرمقدار بین
را اختیار میکند, هرمقدار بین
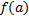 و
و
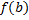 را به خود میگیرد. در نمونه زیر, اهمیت پیوستگی
را به خود میگیرد. در نمونه زیر, اهمیت پیوستگی
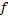 روی
روی
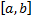 نشان داده میشود.
نشان داده میشود.
مثال 3 : فرض کنید تابع
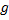 به صورت زیر تعریف شده باشد:
به صورت زیر تعریف شده باشد:
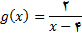
نمودار این تابع در شکل زیر نشان داده شده است.
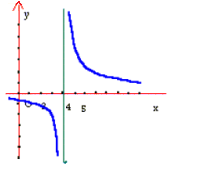
تابع
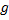 در 4, که در بازه بسته
در 4, که در بازه بسته
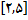 قرار دارد, ناپیوسته است,
قرار دارد, ناپیوسته است,
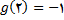 و
و
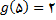 . اگر عدد دلخواهی بین
. اگر عدد دلخواهی بین 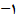 و 2 باشد , هیچ مقداری از
و 2 باشد , هیچ مقداری از
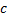 بین 2 و 5 وجود ندارد که
بین 2 و 5 وجود ندارد که
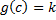 . بخصوص , اگر
. بخصوص , اگر
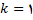 , آنگاه
, آنگاه
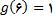 , ولی 6 در بازه
, ولی 6 در بازه
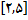 قرار ندارند.
قرار ندارند.
مثال 4: اگر
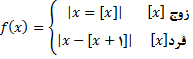
نمودار تابع را رسم کنید. تابع
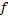 در چه مقادیری از
در چه مقادیری از
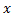 ناپیوسته است.
ناپیوسته است.
حل:
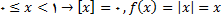 و اگر
و اگر
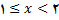 باشد
باشد 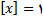 فرد است.
فرد است.
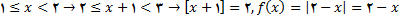
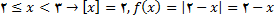
اگر
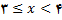 باشد
باشد
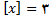 فرد می باشد لذا
فرد می باشد لذا
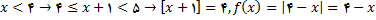
اگر
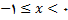 باشد
باشد
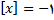 که فرد می باشد پس
که فرد می باشد پس
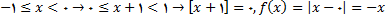
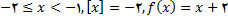
اگر
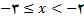 باشد
باشد
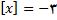 و فرد می باشد و داریم
و فرد می باشد و داریم
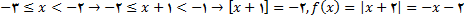
شکل تابع به صورت زیر است
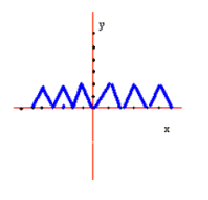
در تمرینهای زیر توابع
در تمرینهای زیر , تعیین کنید که تابع داد شده روی آنها پیوسته است.
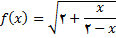
2.
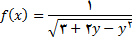
3.
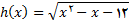
مقادیری برای ثابتهای c و k بیابید که تابع روی
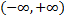 پیوسته باشد و نمودار را رسم کنید
پیوسته باشد و نمودار را رسم کنید
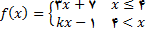
5.
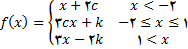
در تمرین های زیر تعین کنید که قضیه مقدار میانی برای مقادیر دادده شده kبرقرار است یا خیر اگر برقرار بود عدد c را بیابید که به ازای آن
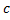 مقدار k معتبر باشد.
مقدار k معتبر باشد.
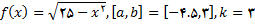
7.