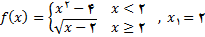مشتق پذیری و پیوستگی
تابع مثال 1 از بخش قبل, در نقطه صفر پیوسته است ولی در آنجا مشتق پذیر نیست. نمودار این تابع در مبدا, بر محور
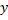 مماس است. در نمونه زیر, تابعی داریم که در نقطه صفر پیوسته است ولی مشتق پذیر نیست و بر نمودارش در مبدا, خطی مماس نمی شود.
مماس است. در نمونه زیر, تابعی داریم که در نقطه صفر پیوسته است ولی مشتق پذیر نیست و بر نمودارش در مبدا, خطی مماس نمی شود.
نمونه1: فرض کنید
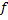 تابع قدر مطلق باشد. بنابراین
تابع قدر مطلق باشد. بنابراین
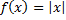 نمودار این تابع در مثال بخش به دست آمد. در اینجا این نمودار در شکل زیر نشان داده می شود. با توجه به فرمول 3 از بخش قبل
نمودار این تابع در مثال بخش به دست آمد. در اینجا این نمودار در شکل زیر نشان داده می شود. با توجه به فرمول 3 از بخش قبل
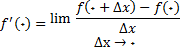
شرطی که این حد موجود باشد. چون
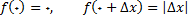
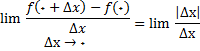
اگر
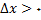 داریم
داریم
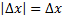 و اگر
و اگر
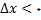 داریم
داریم
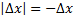 پس باید حدهای یک طرفه در صفر را درنظر بگیریم
پس باید حدهای یک طرفه در صفر را درنظر بگیریم
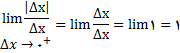
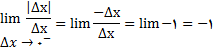
چون
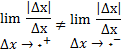
, نتیجه می شود که حد دو طرفه
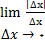 وجود ندارد. بنابراین
وجود ندارد. بنابراین
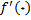 وجود ندارد و لذا
وجود ندارد و لذا
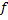 در صفر مشتق پذیر نیست. چون
در صفر مشتق پذیر نیست. چون
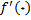 وجود ندارد و نه
وجود ندارد و نه
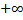 است و نه
است و نه
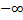 هیچ خطی بر نمودار تابع قدر مطلق در مبدا مماس نمی شود.
هیچ خطی بر نمودار تابع قدر مطلق در مبدا مماس نمی شود.
چون توابع مذکور در نمونه فوق, در یک عدد پیوسته اند اما در ان عدد مشتق پذیر نیستند, میتوان نتیجه گرفت که پیوستگی یک تابع در یک عدد, مشتق پذیری قطعا مستلزم پیوستگی است.
قضیه 1 : اگر تابع
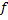 در
در 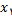 مشتق پذیر باشد, انگاه
مشتق پذیر باشد, انگاه
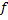 در
در
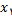 پیوسته است. تابعی چون
پیوسته است. تابعی چون
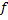 میتواند به یکی از دلایل زیر در عددی مانند
میتواند به یکی از دلایل زیر در عددی مانند
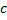 مشتق پذیر نباشد.
مشتق پذیر نباشد.
1 - تابع
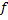 در
در
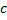 پیوسته نباشد. این موضوع از قضیه نتیجه می شود. برای دیدن نمودار چنین تابعی, به شکل زیر مراجعه کنید.
پیوسته نباشد. این موضوع از قضیه نتیجه می شود. برای دیدن نمودار چنین تابعی, به شکل زیر مراجعه کنید.
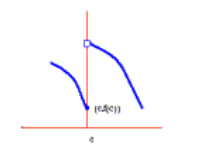
2 -
تابع 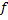 در
در
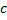 پیوسته باشد و خط قائم بر نمودار
پیوسته باشد و خط قائم بر نمودار
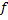 در نقطه به طول
در نقطه به طول 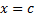 مماس شود. برای دیدن نمودار تابعی که چنین خاصیتی داشته باشد به شکل فوق مراجعه شود.
مماس شود. برای دیدن نمودار تابعی که چنین خاصیتی داشته باشد به شکل فوق مراجعه شود.
3 - تابع
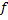 در
در 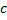 پیوسته باشد, و نمودار تابع
پیوسته باشد, و نمودار تابع
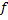 در نقطه به طول
در نقطه به طول
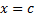 خط مماس نداشته باشد.
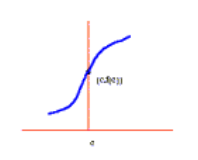
در شکل زیر نمودار تابعی آمده است که در این شرط صدق می کند. ملاحظه می کنید که نمودار در
خط مماس نداشته باشد.
در شکل زیر نمودار تابعی آمده است که در این شرط صدق می کند. ملاحظه می کنید که نمودار در 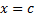 گوشه ای دارد. در نمونه 1, مثال دیگری از این گونه توابع امده است.
گوشه ای دارد. در نمونه 1, مثال دیگری از این گونه توابع امده است.
قبل از ارائه مثال دیگری از تابعی که در یک عدد پیوسته است ولی در آن عدد مشتق پذیر نیست, مفهوم مشتق یک طرفه را تعریف میکنیم.
تعریف 1 : اگر تابع
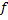 در
در
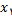 تعریف شده باشد, انگاه مشتق راست
تعریف شده باشد, انگاه مشتق راست
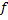 در
در
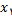 با
با
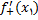 نشان داده می شود و به صورت زیر تعریف می گردد
نشان داده می شود و به صورت زیر تعریف می گردد
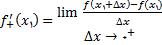 (4)
(4)
و به عبارت دیگر
 (5)
(5)
به شرطی که این حد وجود داشته باشد.
تعریف 2: اگر تابع
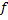 در
در
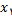 تعریف شده باشد, انگاه مشتق چپ
تعریف شده باشد, انگاه مشتق چپ
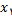 در
در
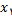 با
با
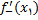 نمایانده میشود و به صورت زیر تعریف می شود.
نمایانده میشود و به صورت زیر تعریف می شود.
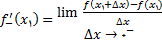 (6)
(6)
و به عبارت دیگر
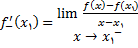 (7)
(7)
به شرطی که این حد وجود داشته باشد.
مثال 3 : فرض کنید 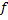 به صورت زیر تعریف شده است
به صورت زیر تعریف شده است
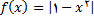
الف ) نمودار تابع 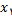 رسم کنید.
رسم کنید.
ب) ثابت کنید که 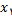 در 1 پیوسته است.
در 1 پیوسته است.
پ) آیا 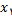 در 1 مشتق پذیر است؟
در 1 مشتق پذیر است؟
حل: بنا به تعریف قدر مطلق اگر
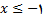 یا
یا
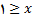 آنگاه
آنگاه
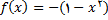 و اگر
و اگر
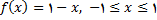 پس
پس 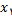 را می توان به صورت زیر تعریف کرد
را می توان به صورت زیر تعریف کرد
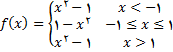
الف) نمودار تابع 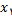 در شکل زیر رسم شده است
در شکل زیر رسم شده است
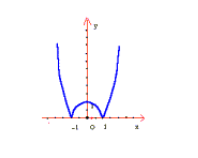
ب) برای اثبات اینکه در 1 پیوسته است سه شرط پیوستگی را بررسی میکنیم
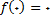 .1
.1
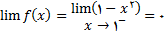 .2
.2
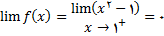
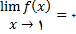
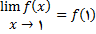 .3
.3
چون شرطهای 1 تا 3 همگی در یک برقرارند, پس 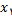 در 1 پیوسته است.
در 1 پیوسته است.
پ)
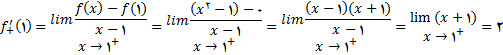
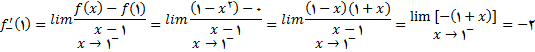
چون 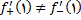 , پس
, پس
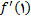 وجود ندارد و بنابراین ,
وجود ندارد و بنابراین , 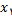 در 1 مشتق پذیر نیست با استفاده از روشی مشابه, میتوان نشان داد که تابع مثال 2 در
در 1 مشتق پذیر نیست با استفاده از روشی مشابه, میتوان نشان داد که تابع مثال 2 در
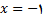 نیز مشتق پذیر نیست.
نیز مشتق پذیر نیست.
مثال:
اگر 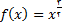 باشد. ثابت کنید تابع
باشد. ثابت کنید تابع 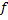 از سمت راست در صفر پیوسته است و
از سمت راست در صفر پیوسته است و
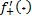 وجود دارد.
وجود دارد.
حل: چون
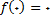 و
و
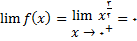 بنابراین تابع از سمت راست و از طرفی
بنابراین تابع از سمت راست و از طرفی
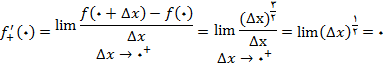
پس 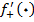 موجود و برابر صفر است.
موجود و برابر صفر است.
در هر یک از تمرینهای زیر اعمال زیر ر انجام دهید:
الف ) نمودار تابع را رسم کنید.
ب) معین کنید که 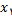 در
در
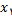 پیوسته است یا خیر
پیوسته است یا خیر
پ) 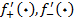 را درصورت وجود محاسبه کنید.
را درصورت وجود محاسبه کنید.
ت) تعین کنید که 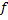 در
در
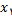 مشتق پذیر است یا خیر
مشتق پذیر است یا خیر
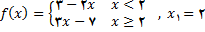
2.
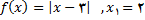
3.
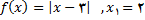
4.